PLANETCALC Calculatrices en ligne

S'identifier
Las étudeMathGéométrie

Découpe d'un cercle

Deux manières de découper un cercle en parties égales : découpes par secteur et découpes parallèles.

Cette page existe grâce aux efforts des personnes suivantes :

Timur

Timur

GM

Gaulthier Marrel

Créé: 2021-05-25 04:26:17, Dernière mise à jour: 2021-05-27 04:19:25
Creative Commons Attribution/Share-Alike License 3.0 (Unported)

Ce contenu est sous License Creative Commons Attribution/Partage à l'Identique 3.0(Unported). Cela signifie que vous pouvez redistribuer ou modifier librement ce contenu avec les mêmes modalités de licence et que vous devez créditer l'auteur original en plaçant un lien hypertexte de votre site vers l'œuvre https://fr.planetcalc.com/8943/. Vous ne pouvez pas modifier (le cas échéant) les références dans le contenu de l'œuvre originale.

Ci-dessous, vous pouvez trouver deux calculateurs qui calculent comment découper un cercle en parties égales : une manière traditionnelle et une non-traditionnelle. Par manière traditionnelle, je veux dire découper un cercle en secteurs, tout comme vous découpez généralement une tarte ou une pizza. Et par manière non-traditionnelle, je veux dire découper un cercle en parts verticales égales avec des lignes parallèles ou avec des cordes parallèles, si vous préférez. Les deux calculateurs présentent un dessin illustrant le résultat. Et vous pouvez trouver toutes les formules et calculs dans l'article en-dessous du calculateur.

PLANETCALC, Découper un cercle en secteurs égaux

Découper un cercle en secteurs égaux

Chiffres après la virgule décimale : 2
Angle d'un secteur
 
Longueur de l'arc d'un secteur
 
Longueur de la corde d'un secteur
 

PLANETCALC, Découper un cercle en partie égales avec des découpes parallèles

Découper un cercle en partie égales avec des découpes parallèles

Chiffres après la virgule décimale : 2
Le fichier est très volumineux; un ralentissement du navigateur peut se produire pendant le chargement et la création.

Découper un cercle en secteurs

Bien, vous devez découper un cercle en plusieurs secteurs (nombres pairs et impairs). Pour faire ceci, vous devez trouver les paramètres d'un secteur. C'est une tâche simple :

  1. Trouver l'angle d'un secteur en radians, en divisant 2π (représentant 360 degrés en radians) par un nombre de secteurs.

\alpha=\frac{2\pi}{N}

  1. Trouver la longueur de l'arc d'un secteur en multipliant le rayon par l'angle d'un secteur en radians.

a=\alpha R

  1. Trouver la longueur de la corde d'un secteur en utilisant la loi des cosinus (une corde est la base du triangle isocèle, avec deux rayons comme côté égaux et l'angle du secteur comme angle de sommet).

c=R^2+R^2-2RR \cos \alpha

Ceci définit complètement les N secteurs égaux.

Découper en cercle avec des coupes parallèles

Cette manière est plus intéressante. Pour plus de simplicité, je considérerai un demi-cercle puisqu'il est symétrique.

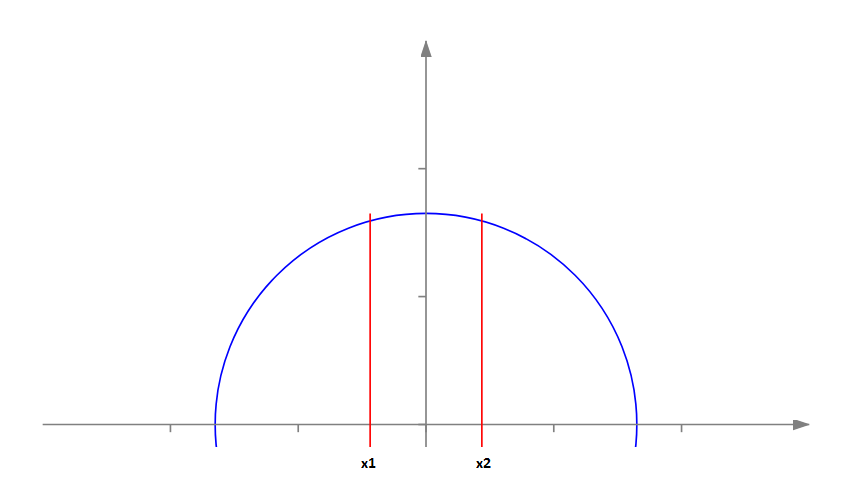
Découpe d'un cercle en trois parties avec deux lignes parallèles
Découpe d'un cercle en trois parties avec deux lignes parallèles

Découpons-le en parts verticales. Dans ce cas, nous avons besoin de trouver les coordonnées x des cordes parallèles qui doivent diviser notre cercle en parties de surface égale. (voir les points x1 et x2 sur l'image ci-dessus). Dérivons la formule général pour une surface du côté gauche.

Notre demi-cercle peut être vu comme une fonction y=f(x), où x - est la coordonnée le long de l'axe des abscisses et y est la fonction égale à la valeur du point du demi-cercle correspondant.

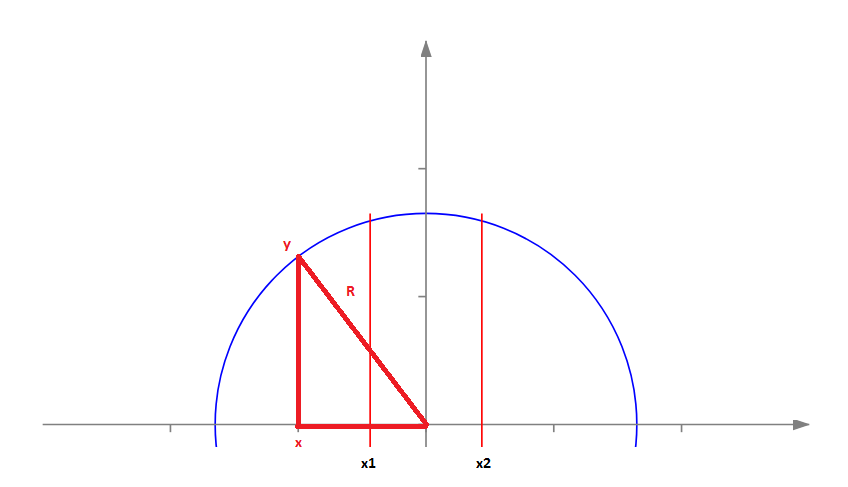
y=f(x)
y=f(x)

En utilisant le théorème de Pythagore, la fonction y est

y=\sqrt{R^2 - x^2}}

Pour trouver une surface du côté gauche, vous devez intégrer cette fonction de -R à x. La primitive de notre fonction est :

F(x)=\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+C

Nous devons trouver la valeur d'une constance. Manifestement, au point où x est égale à -R où la surface doit être nulle. Si nous insérons -R plutôt que x dans le formule ci-dessus, nous obtenons

F(-R)=-\frac{\pi R^2}{4}+C=0, ainsi

C=\frac{\pi R^2}{4}

Notre intégrale finale est

F(x)=\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}

Maintenant, comment trouvons nous x pour la première découpe ? Nous connaissons la surface que nous devons obtenir - N-ième partie de la surface totale (pas le demi-cercle)

S=\frac{\frac{\pi R^2}{2}}{N}=\frac{\pi R^2}{2N}

Ainsi, nous pouvons égaler

\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}=\frac{\pi R^2}{2N}

Ce qui nous donne

\frac{1}{2} (x\sqrt{R^2-x^2} + R^2 \arctan(\frac{x}{\sqrt{R^2-x^2}}))+\frac{\pi R^2}{4}-\frac{\pi R^2}{2N}=0

Ceci est une équation transcendantale et nous devons utiliser des méthodes numériques pour la résoudre, par exemple Méthode de la bissection ou Méthode de newton. Ici, nous utilisons la méthode de Newton.

Le point de découpe suivant peut être trouvé avec la même approche. Nous devons découper deux fois de plus pour le deuxième point S_2=2\frac{\pi R^2}{2N}, trois fois de plus pour le troisième point S_3=3\frac{\pi R^2}{2N} et ainsi de suite.

Ensuite, nous pouvons trouver tous les autres paramètres, tels que la longueur de la corde, en utilisant les coordonnées du point.

URL copiée dans le presse-papiers

Calculatrices similaires

 #cercle #géométrie angle arc cercle corde découpe Géométrie parallèle secteur surface
PLANETCALC, Découpe d'un cercle
Timur2021-05-27 04:19:25

commentaires