Intersection de deux cercles
Ce calculateur en ligne trouve les points d'intersection de deux cercles suivant les centres et rayons donnés pour chaque cercle. Il les trace également sur le graphique.
Pour utiliser le calculateur, saisissez les coordonnées x et y du centre et le rayon de chaque cercle.
Un peu de théorie est disponible en-dessous du calculateur.
Intersection de cercles
La tâche est relativement simple, mais nous devons tenir compte des cas limites, ainsi, nous devrions commencer par calculer la distance cartésienne d entre les deux centres et vérifier les cas limites en comparant d avec les rayons r1 et r2
Voici les cas possibles (la distance entre les cercles est illustrée en rouge) :
| Cas | Description | Règle |
|---|---|---|
| Cas trivial : les cercles coïncident (ou c'est le même cercle) | ||
 |
Les cercles sont séparés | |
 |
Un cercle est contenu au sein de l'autre | |

 |
Deux points d'intersection | Vous avez un ou deux points d'interesction si toutes les règles des cas limites ci-dessus ne s'appliquent pas |

 |
Un point d'intersection | Cas trivial de deux points d'intersection |
Ainsi, s'il ne s'agit pas d'un cas limite, pour trouver les deux points d'interesction, la calculateur utilise les formules suivantes (principalement déduites à partir du théorème de Pythagore), illustré par le graphique ci-dessous :
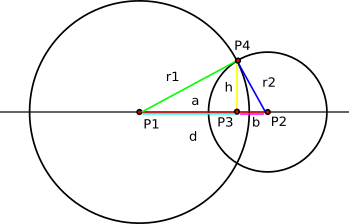
Tout d'abord, le calculateur trouve le segment a
et ensuite le segment h
pour trouver le point P3, le calculateur utilise la formule suivante (sous la forme vectorielle) :
Et finalement, pour obtenir la paire de points dans le cas de deux points d'intersection, le calculateur utilise ces équations :
Premier point :
Deuxième point :
Notez les signes opposé devant la deuxième opérande
Pour plus d'informations, vous pouvez vous référer à Cercle-Intersection de Cercles et Cercles et sphères
Calculatrices similaires
- • Equation d'un cercle suivant un centre et un rayon donnés sous différentes formes
- • Equation d'un cercle passant par 3 points donnés
- • Combien de cercles de rayons r tiennent dans un cercle plus grand de rayon R
- • Centre et rayon d'un cercle en allant de la forme générale à la forme standard
- • Découpe d'un cercle
- • Section Géométrie ( 52 calculatrices )
commentaires