Involute d'un angle
Calculateur de l'involute d'un angle et recherche d'un angle selon son involute donnée.
Dans le thème des engrenages, j'ai découvert les termes involute et développante. Ils sont intéressants et méritent des calculateurs séparés, disponibles ci-dessous. Le premier est pour l'involute et les deux autres sont pour trouver l'angle selon l'involute donnée. Pour les personnes intéressées, le texte sur l'involute est en-dessous des calculateurs.
Involute d’un angle
Trouver un angle suivant son involute (méthode de Laskin)
Trouver un angle selon son involute (méthode de Cheng)
Donc, en géométrie différentielles des courbes développantes, il y a une courbe normale qui est tangente à la courbe d'origine en chaque point (voir Courbe développante).
Comme il est difficile de comprendre tout ce qui précède, je vais redonner une définition figurative telle que disponible dans l'article.
Alors, imaginez, une bobine fil où l'extrémité libre est sur la bobine. Si vous prenez cette extrémité libre et commencez à dérouler la bobine en la gardant serrée, l'extrémité décrira une courbe développante du cercle (la bobine est initialement une courbe qui est un cercle)
Les images suivants décrivent la développante du cercle (Wikipédia). La ligne rouge est une courbe d'origine (cercle), la ligne noire est une bobine étirée, la ligne verte est la trajectoire de l'extrémité de la bobine - la courbe appelée la développante du cercle.
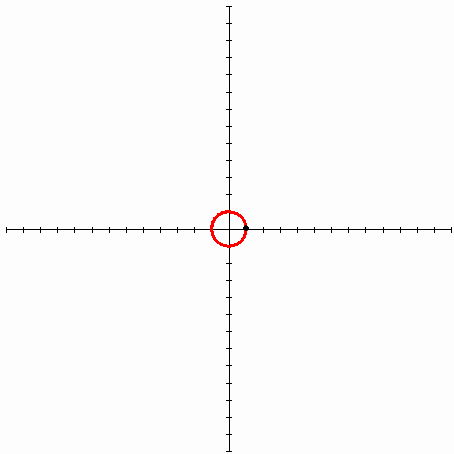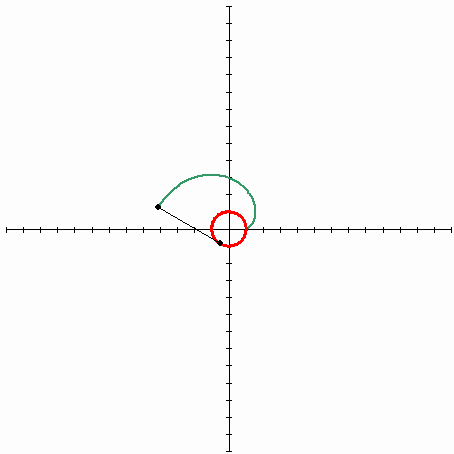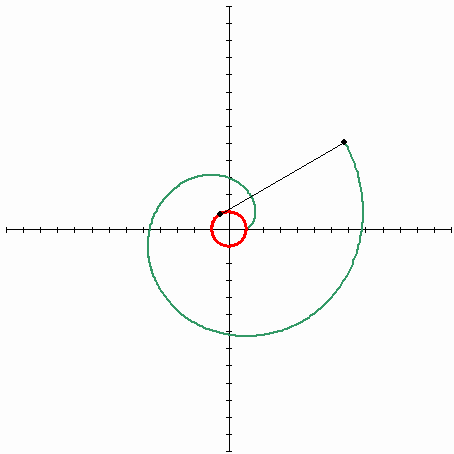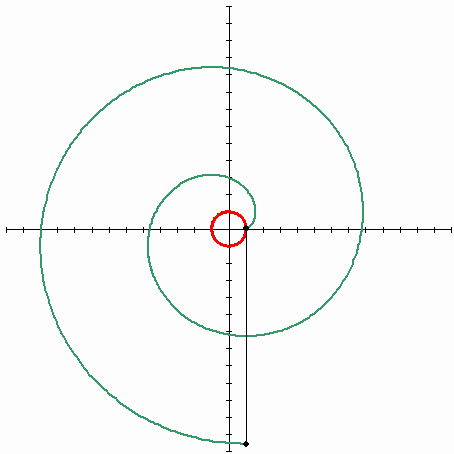
Maintenant voyons le type de fonction dont il s'agit. L'image que j'ai créée aidera :
La section de cette image est égale à l'arc
(car c'est notre "bobine"). L'angle "φ" est égal à l'arc
appelé angle développant du rouleau et consiste en la somme des angles "θ" angle (angle développant) et "α" (angle de pression). La longueur de l'arc est
Comme est un triangle rectangle, ceci signifie que
En égalisant ces deux arcs ensemble, nous obtiendrons, soit
Cette fonction
est appelée involute ou développante de la fonction.
L'équation de la courbe involute en coordonnées polaires ressemble à ceci :
Par construction, nous pouvons voir que l'angle "α" peut varier de 0 à 90 mais en excluant 90 car dans ce cas la ligne droite KK sera parallèle à MxN.
Pourquoi devrions nous faire ceci ? La développante du cercle est utilisé pour l'engrenage involute - l'engranage dont le profil de dents esquisse l'involute du cercle. Durant l'involute de l'engrenage, la normale commune au contact des dents du profil coincide toujours avec la tangente commune du cercle de base. Cette tangente est appelée ligne de pression car le point de contact de chaque dent se déplace sur cette ligne durant le mouvement de la roue.
(image). C'est le type d'engrenage le plus commun.
Et l'involute est utilisée dans les calculs associés à un engrenage involute. De plus, il y a des calculs d'involute et vice versa - trouver un angle selon son involute. Et le second type de calcul n'a pas si simple car l'équation est une équation transcendantale et seules les méthodes numériques peuvent la résoudre.
En résumé, nous reverrons les méthodes numériques utilisées dans les calculateurs ci-dessus - les méthode de Laskin et de Cheng (pour plus d'informations voir ceci)
Méthode de Laskin
Basée sur la méthode de Newton, qui consiste en une procédure de calculs itératifs
Le savoir-faire de cette méthode réside dans le choix des valeurs initiales, qui, avec la méthode de Laskin, sont calculées comme
, où I - valeur initiale de l'involute
Pour calculer l'approximation suivante après la divulgation de la dérivée, nous obtiendrons l'expression
Cinq itérations sont utilisées dans le calculateur, mais quatre fournissent la précision à la sixième décimale. Cette méthode fonctionne pour les valeurs d'involute de 0 à 1, donc vous pouvez trouver les angles de 0 à 64,87 degrés. En pratique, c'est suffisante. Il y a des tableaux pour trouver l'involue qui sont similaires aux tableaux des fonctions trigonométriques et ils ont une gamme d'angles de 0 à 60.
Méthode de Cheng
Basée sur la détermination d'une valeur approximative en utilisant les courbes asymptotiques. Cheng a développé la formule suivante :
Vous pouvez utiliser cette méthode pour trouver les valeurs d'involute qui sont strictement inférieures à 1,8 soit les angles jusqu'à 71,87. Et vous n'avez pas besoin de ces valeurs supérieures, proches de 90, la tangente tend vers l'infini, avec toutes les conséquences qui s'ensuivent. De plus, il n'y a pas d'engrenage à dentes avec des angles aussi importants.
commentaires