Division synthétique
Une méthode simple de division de polynômes.
Ce contenu est sous License Creative Commons Attribution/Partage à l'Identique 3.0(Unported). Cela signifie que vous pouvez redistribuer ou modifier librement ce contenu avec les mêmes modalités de licence et que vous devez créditer l'auteur original en plaçant un lien hypertexte de votre site vers l'œuvre https://fr.planetcalc.com/8091/. Vous ne pouvez pas modifier (le cas échéant) les références dans le contenu de l'œuvre originale.
La division synthétique est une méthode de division euclidienne de polynômes avec peu de rédaction et de calculs.
Ce calculateur réalise la division synthétique euclidienne de polynômes. Vous pouvez trouver la description de la méthode juste en-dessous du calculateur.
Préparation de la division synthétique
La préparation de la division synthétique en exemple : 3x4+5x3+2x+4 / x2+2x+1.
| Étapes de la préparation | |
|---|---|
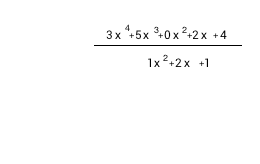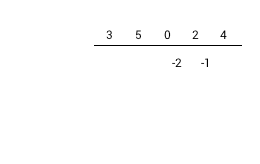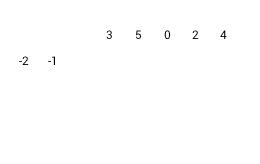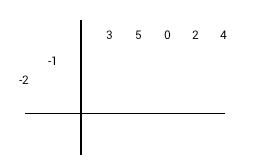 |
1) Coefficients négatifs du diviseur 2) Écrire les coefficients du diviseur en haut (zéro pour les termes manquants). 3) Supprimer le coefficient du diviseur le plus élevé. 4) Écrire les coefficients du diviseur restant, diagonalement à partir de la gauche |
Méthode de division synthétique pour les diviseurs unitaires
La division synthétique avec des diviseurs unitaires en exemple : 3x4+5x3+2x+4 / x2+2x+1.
| Algorithme de division pour les diviseurs unitaires | |
|---|---|
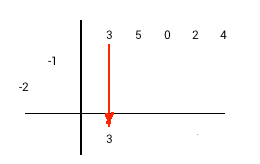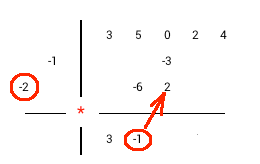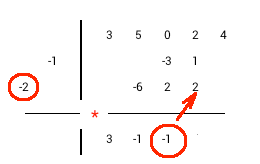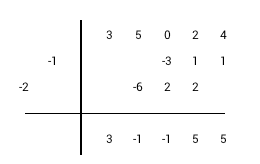 |
1) Faire passer le coefficient du diviseur le plus élevé dans la première colonne de la ligne de résultats 2) Multiplier la diagonale de diviseur par la valeur de la dernière colonne de la ligne de résultats 3) Placer le résultat de la multiplication diagonalement à droite de la dernière colonne de résultats 4) Réaliser l'addition dans la colonne suivante et écrire la somme dans la même colonne de la ligne de résultats 5) Répéter les étapes 2 à 4 jusqu'à ce que vous passiez à la colonne en haut de la ligne. 6) Additionner les valeurs dans chaque colonne restante et écrire le résultat dans la ligne de résultats. 7) Séparer le résultat et le reste. Le nombre de termes du reste est égale au nombre de termes du diviseur moins un. |
Diviseurs non-unitaires
La division synthétique avec des diviseurs non-unitaires en exemple : 3x3+5x2+7x+2 / 3x2-x-2.
| Algorithme de division pour les diviseurs non-unitaires | |
|---|---|
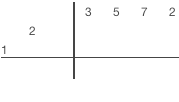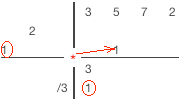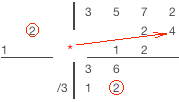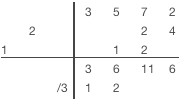 |
1) Faire passer le coefficient du diviseur le plus élevé dans la première colonne de la ligne de restes 2) Diviser la dernière colonne de la ligne de reste par le premier coefficient du diviseur, écrire le résultat dans la ligne de résultats 3) Multiplier la diagonale du diviseur par la valeur de la dernière colonne de la ligne de résultats 4) Placer le résultat de la multiplication diagonalement à droite de la dernière colonne de résultats 5) Réaliser l'addition dans la colonne suivant et écrire la somme dans la même colonne de la ligne de restes 6)Répéter les étapes 2 à 5 jusqu'à ce que vous passiez la colonne de la ligne du haut. 6) Additionner les valeurs dans chaque colonnes restantes et écrire le résultat dans la ligne de restes. 7)Séparer le résultat et le reste. Le coefficient du résultat sera dans la dernière ligne. Les coefficients des restes seront dans la ligne précédente. le nombre de termes du reste est égale au nombres de termes du diviseur moins un. |
commentaires