PLANETCALC Calculatrices en ligne

S'identifier
Las étudePhysique

Les ondes et le vent. Calcul des caractéristiques des ondes

Calcul des caractéristiques des ondes

L'intuition suggère qu'il y a une certaine relation entre la force du vent et les ondes. Comme je ne connais pas bien la théorie des ondes, j'ai du l'étudier.
Le résultat de mes études est le calculateur ci-dessous ainsi que mes réflexions sur le sujet. Le calculateur ne calcul pas, ou plus précisément ne prédit pas la hauteur des ondes - c'est un autre problème qui est revu ici Les ondes et le vent.

PLANETCALC, Calcul de la performance des ondes

Calcul de la performance des ondes

Chiffres après la virgule décimale : 2
Profondeur relative
 
Longueur de l'onde (mètres)
 
Fréquence angulaire (rad/s)
 
Nombre d'ondes
 
Vitesse de phase (m/s)
 
Vitesse de groupe (m/s)
 

Théorie

Il est assez évident que les ondes sur la mer ne peuvent pas être décrites par une seule onde sinusoïdale puisqu'elles résultent de plusieurs ondes avec différentes périodes et phases. Par exemple, regardez l'image ci-dessous qui montre l'onde résultante de l'imposition de trois ondes sinusoïdales différentes.

"Affichage des ondes" par Kraaiennest - Création personnelle. Sous licence GFDL via Wikimédia Commons - http://commons.wikimedia.org/wiki/File:Wave_disp.gif#mediaviewer/File:Wave_disp.gif
"Affichage des ondes" par Kraaiennest - Création personnelle. Sous licence GFDL via Wikimédia Commons - http://commons.wikimedia.org/wiki/File:Wave_disp.gif#mediaviewer/File:Wave_disp.gif



Source : "Affichage des ondes" par Kraaiennest - Création personnelle. Sous licence GFDL via Wikimédia Commons - http://commons.wikimedia.org/wiki/File:Wave_disp.gif#mediaviewer/File:Wave_disp.gif

Ainsi, pour analyser l'état de la mer, le spectre d'énergie est généralement développé, soit les unités d'énergie réparties sur l'axe Y et la fréquence sur l'axe X, obtenant ainsi la densité énergétique - la quantité d'énergie transportée par les ondes avec une gamme de fréquence correspondante. Et, comme il s'est avéré, sous l'influence du vent, la forme et le spectre d'énergie sont modifiés, plus le vent est fort, plus le pic du spectre est exprimé de manière importante - les ondes de certaines fréquences transportant le plus d'énergie. Sur l'image ci-dessous, j'ai dessiné son aspect approximatif du mieux que j'ai pu.

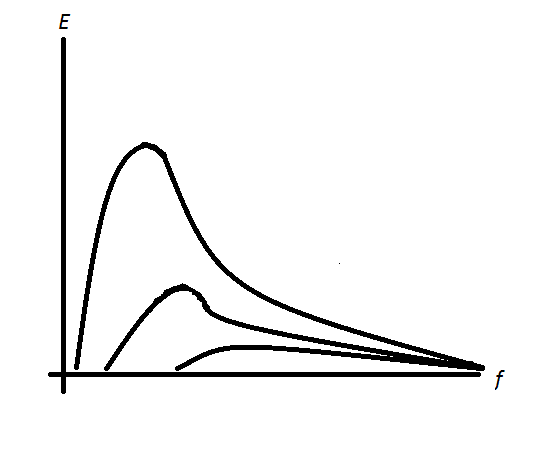
La distribution énergétique du spectre de fréquences, suivant la force du vent
La distribution énergétique du spectre de fréquences, suivant la force du vent

Les fréquences où le pic est observé sont appelées dominantes. En conséquence, vous pouvez vous faciliter la vie et calculer les caractéristiques des ondes pour le fréquence dominante uniquement. La pratique a montré que c'est suffisant pour donner une bonne approximation de la réalité.

En ce qui concerne les caractéristiques des ondes, la théorie des ondes linéaires est utile, en d'autres mots le calcul des ondes gravitationnelles dans l'approximation linéarisée. Pour définir plus clairement ce que je signifie, voici davantage de définitions issues de wikipédia :

Ondes capillaires —le nom de diverses ondes générées à l'interface entre un liquide et un gaz ou entre deux liquides. La partie inférieure de l'onde est appelée creux, la plus élevée — crête.

Ondes de gravité sur l'eau — type d'onde à la surface d'un liquide dans lequel la force renvoyant la surface déformée du liquide dans un état d'équilibre est simplement la force de gravité en lien avec la différence de hauteur entre les crêtes et les creux dans le champ de pesanteur.

Dispersion des ondes — dans la théorie des ondes différences de vitesses de phase des ondes linéaires suivant leur fréquence. Soit, les longueurs d'ondes différents (respectivement de fréquences différentes) ont des vitesses différentes dans un environnement qui a clairement prouvé l'expérience de la réfraction de la lumière dans un prisme. C'est important pour une discussion approfondie

Nombre d'ondes — c'est les 2π radians suivant le rapport de la longueur d'onde : k \equiv \frac{2\pi}{\lambda}.Le nombre d'ondes peut être représenté comme la différence de la phase de l'onde (en radians) au même moment dans le temps que les points spatiaux à une distance par unité de longueur (un mètre) ou un nombre de périodes spatiales (crêtes) où les ondes arrivent à 2π mètres.

En utilisant la définition du nombre d'ondes, nous pouvons écrire les formules suivantes :

Longueur d'onde
\lambda=\frac{2\pi}{k}

Vitesse de phase (vitesse de crête )
c=\frac{\omega}{k}

Période de l'onde(exprimée en terme de fréquence angulaire)
T=\frac{2\pi}{\omega}

Image pour attirer l'attention - les points montrent la vitesse de phase, vert - la vitesse de groupe (la vitesses de paquets d'ondes)

"Groupe d'ondes" par Kraaiennest - Création personnelle. Sous licence GFDL via Wikimédia Commons - http://commons.wikimedia.org/wiki/File:Wave_group.gif#mediaviewer/File:Wave_group.gif
"Groupe d'ondes" par Kraaiennest - Création personnelle. Sous licence GFDL via Wikimédia Commons - http://commons.wikimedia.org/wiki/File:Wave_group.gif#mediaviewer/File:Wave_group.gif



Source : "Groupe d'ondes" par Kraaiennest - Création personnelle. Sous licence GFDL via Wikimédia Commons - http://commons.wikimedia.org/wiki/File:Wave_group.gif#mediaviewer/File:Wave_group.gif

La loi de dispersion

L'élément clef du calcul des caractéristiques des ondes est le concept de la loi de dispersion ou de la relation de dispersion (rapport)

La loi de dispersion ou équation de dispersion(rapport) dans la théorie des ondes - est la relation entre la fréquence et le vecteur de l'onde (nombre d'ondes).

En terme général, cette relation est écrite comme
\omega=f(k).

Ce rapport d'eau dérivé de la théorie des ondes linéaires pour la surface considérée comme libre est la surface du liquide ne se limitant pas aux parois de la cuve ou du lit et ressemble à ce qui suit :
\omega^2=gk \tanh(kh),
où
g - accélération de chute libre
k - nombre d'ondes,
tanh - tangente hyperbolique,
h - distance de la surface du liquide jusqu'au fond.

Il est possible de simplifier davantage la formule, sur la base du graphique de la tangente hyperbolique. Notez que pour que kh tendant vers zéro, la tangente hyperbolique peut être approximée par son argument, soit la valeur de kh, et si kh tend vers l'infini, la tangente hyperbolique tend vers un. Evidemment, dans le dernier cas, cela est pour une très grande profondeur. Est-il possible d'évaluer l'importance de la profondeur nécessaire ? Si vous prenez la tangente hyperbolique de pi alors sa valeur est approximativement égale à 0,9964, ce qui est déjà très proche de un (le nombre Pi est pris pour faciliter la formule). Ensuite
kh\geq\pi \Rightarrow \frac{2 \pi h}{\lambda}\geq\pi \Rightarrow h\geq\frac{\lambda}{2}.
Ainsi, pour calculer les caractéristiques de l'onde, l'eau peut être considérée comme profonde si la profondeur est supérieure à au moins la moitié de la longueur d'onde, dans la plupart des océans du monde, cette condition est respectée.

En général, sur la base du graphique d'une tangente hyperbolique, la classification suivante des ondes suivant leur profondeur relative est utilisée (rapport de la profondeur et de la longueur de l'onde).

1. Ondes en eau profonde
La profondeur est supérieure à la moitié de la longueur de l'onde, la tangente hyperbolique est approximée par un
h\geq\frac{\lambda}{2}, \tanh(kd)\approx1

2. Ondes sur les profondeurs de transition
La profondeur est entre un vingtième et la moitié de la longueur de l'onde, la tangente hyperbolique ne peut pas être approximée
\frac{\lambda}{20} \leq h \leq \frac{\lambda}{2}, \tanh(kd)=\tanh(kd)

3. Ondes en eau peu profonde
La profondeur est inférieure à un vingtième de la longueur de l'onde, la tangente hyperbolique est approximée par son argument
h\leq\frac{\lambda}{20}, \tanh(kd)=kd

Considérer le rapport pour ces cas

Le cas des eaux peu profondes

L'équation prendre la forme
\omega^2=gk(kh)=ghk^2,
d'où
c=\sqrt{gh}
\lambda=T\sqrt{gh}

la vitesse du groupe dans le cas d'eau peu profonde
c_g=c=\sqrt{gh}

Ainsi, suivant la théorie, en eau peu profonde, l'onde n'a pas de dispersion car la vitesse de phase est indépendante de la fréquence. Cependant, nous devons nous rappeler qu'en eau peu profonde, les effets non-linéaires de l'eau commencent à entrer en action en lien avec l'augmentation de l'amplitude de l'onde. L'impact des effets non-linéaires, lorsque l'amplitude de l'onde est comparable à sa longueur. L'un des effets caractéristiques dans ce mode est l'apparition de fractures sur les arrêts d'ondes. De plus, il y a la possibilité de rupture d'onde, bien connue pour le surf. Ces effets ne sont pas encore prêts pour des calculs analytiques précis.

Cas des profondeurs de transition

L'équation n'est pas simplifiée, et donc
c=\frac{gT}{2\pi}\tanh(\frac{2\pi d}{\lambda})
\lambda=\frac{gT^2}{2\pi}\tanh(\frac{2\pi d}{\lambda})

La vitesse du groupe pour les profondeurs de transition
c_g=\frac{1}{2}(1+\frac{4 \pi \frac{d}{\lambda}}{\sinh(4 \pi \frac{d}{\lambda})})c

Notez que l'équation de la longueur d'onde est transcendental et sa solution doit être trouvée numériquement. Par exemple en utilisant Méthode d'itération du point fixe

Cas des eaux profondes

L'équation prend la forme
\omega^2=gk,
d'où
c=\frac{gT}{2\pi}
\lambda=\frac{gT^2}{2\pi}

La vitesse du groupe pour les eaux profondes
c_g=\frac{1}{2}c=\frac{gT}{4\pi}

Ainsi, en mesurant la période d'une onde avec suffisamment de précision, nous pouvons calculer la vitesse de phase, la vitesse du groupe et la longueur d'onde. Et la mesure de la période de l'onde peut être par exemple faite en chronométrant le temps de passage des crêtes de l'onde avec un chronomètre, soit la période - c'est la chose la plus raisonnable qui puisse être mesurée sans instrument spécial. Si vous êtes près des côtes, il est nécessaire d'imaginier la profondeur et si elle est manifestement importante, vous pouvez utiliser les formules pour les eaux profondes, dans lesquelles, la profondeur n'est pas incluses en tant que paramètre. Comme nous avons la puissance de calcul d'un ordinateur à disposition, le calculateur n'utilise pas la formule simplifiée et trouve la longueur d'onde par la méthode d'itération (la méthode convergera comme la dérivé de la fonction et inférieure à un).

Maintenant, revenons au vent. En fait, un vent soufflant constamment dans une direction est ce qui génère l'onde, et donc apporte de l'énergie à l'onde.
Et bien évidemment, afin d'apporder de l'énergie aux ondes, le vent doit souffler plus fort ou au moins à une vitesse égale à la vitesse de phase de l'onde.

Voici, des formules marines entièrement développées. Mer complètement développée - onde qui atteint la valeur maximale pour un vent donné. Ainsi, l'onde est à l'équilibre d'un point de vue énergétique - tant que l'énergie est apportée et que le mouvement a lieu. Toutes les ondes n'atteignent pas cet état, car il nécessite que le vent souffle constamment sur toute la surface par laquelle l'onde passe pendant un certain temps. Et plus le vent est fort, plus le temps et la distance nécessaire pour la formation d'une telle onde sont importants. Mais assurément, quand elle est formée elle rattrapera la vitesse de phase de la vitesse du vent.

URL copiée dans le presse-papiers

Calculatrices similaires

 fréquence fréquence angulaire hydrodynamique longueur longueur de l'onde longueur des ondes mécanique des fluides nombre d'ondes période de l'onde période des ondes Physique vitesse vitesse de phase
PLANETCALC, Les ondes et le vent. Calcul des caractéristiques des ondes
Timur2021-01-27 03:10:14

commentaires