Calotte et segment sphériques
Ce calculateur calcule le volume et l'aire de la surface d'une calotte et d'un segment sphériques.
Ce contenu est sous License Creative Commons Attribution/Partage à l'Identique 3.0(Unported). Cela signifie que vous pouvez redistribuer ou modifier librement ce contenu avec les mêmes modalités de licence et que vous devez créditer l'auteur original en plaçant un lien hypertexte de votre site vers l'œuvre https://fr.planetcalc.com/283/. Vous ne pouvez pas modifier (le cas échéant) les références dans le contenu de l'œuvre originale.

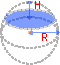
Une calotte sphérique est la région d'une sphère qui est au-dessus (ou en-dessous) d'un plan donné. Si le plan passe par le centre de la sphère, la calotte est appelée hémisphère.
Formules :
- aire de la surface latérale
- aire de la surface de base
- volume

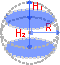
Un segment sphérique est le solide défini en coupant la sphère avec une paire de plans parallèles. Il peut être vu comme une calotte sphérique avec le haut tronqué, et il correspond donc à un cône sphérique.
Formules :
- aire de la surface latérale
- volume
commentaires