Calculatrice en ligne: Valeurs du triangle selon les coordonnées des sommets

Valeurs du triangle selon les coordonnées des sommets

Ce calculateur en ligne calcule un ensemble de valeurs du triangle : longueurs des côtés, angles, périmètre et surface selon les coordonnées de ses sommets

Ce calculateur en ligne est conçu pour calculer rapidement un nombre de caractéristiques d'un triangle selon les coordonnées de ses sommets. Vous saisissez les coordonnées des sommets A, B et C. Le calculateur calcule les valeurs suivantes à partir des coordonnées :

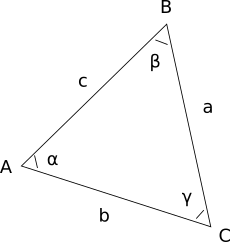
la longueur du côté a - le côté opposé au sommet A
la longueur du côté b - le côté opposé au sommet B
la longueur du côté c - le côté opposé au sommet C
la valeur de l'angle α au sommet A
la valeur de l'angle β au sommet B
la valeur de l'angle γ au sommet C
le périmètre du triangle
surface d'un triangle

Si vous avez besoin de quelque chose d'autres, écrivez-le dans les commentaires, nous l'ajouterons. Les formules pour le calcul des valeurs du triangle sont décrites sous le calculateur.

Valeurs du triangle selon les coordonnées des sommets

Sommet A

x₁

y₁

Sommet B

x₂

y₂

Sommet C

x₃

y₃

Précision de calcul

Chiffres après la virgule décimale : 2

Côté a

Côté b

Côté c

Angle α

Angle β

Angle γ

Périmètre

Surface

Calcul d'un triangle selon les coordonnées de ses sommets

Les longueurs des côtés sont trouvées selon la formule pour calculer la distance entre des points en coordonnées cartésiennes
$c = l_ {AB} = \ sqrt {(x_2-x_1) ^ 2 + (y_2-y_1) ^ 2}$

Les angles sont issus des formules du produit scalaire des vecteurs aux sommets.
$\mathbf {a} \cdot \mathbf {b} =\|\mathbf {a} \|\ \|\mathbf {b} \|\cos \gamma$

Le périmètre est trouvé en ajoutant simplement les longueurs des côtés.
$P = a + b + c$

La surface d'un triangle est trouvée via le déterminant
$S=\pm \frac{1}{2} \left| \begin{matrix} x_1 - x_3 & y_1 - y_3 \\ x_2 - x_3 & y_2 - y_3 \end{matrix} \right|=\pm \frac{1}{2} \left( (x_1 - x_3)(y_2 - y_3) - (y_1 - y_3)(x_2 - x_3) \right)$

PLANETCALC Calculatrices en ligne

Valeurs du triangle selon les coordonnées des sommets

Cette page existe grâce aux efforts des personnes suivantes :

Timur

Gaulthier Marrel

Valeurs du triangle selon les coordonnées des sommets

Sommet A

Sommet B

Sommet C

Calcul d'un triangle selon les coordonnées de ses sommets

Calculatrices similaires

commentaires

PLANETCALC Calculatrices en ligne

Valeurs du triangle selon les coordonnées des sommets

Sommet A

Sommet B

Sommet C

Calcul d'un triangle selon les coordonnées de ses sommets

Calculatrices similaires

commentaires

Partager la page