Calculateur pour spirale
Ce calculateur en ligne calcule les dimensions inconnues d'une spirale d'Archimède à partir des dimensions connues. Les dimensions de la spirale incluent : diamètre externe, diamètre interne, distance de séparation (distance entre deux bras, épaisseur), longueur de la spirale, nombre de tours
Ceci est un calculateur universel pour la spirale d'Archimède.

Nous avons cinq dimensions pour la spirale : diamètre externe - D, diamètre interne - d, épaisseur, distance de séparation ou distance entre les bras - t, longueur de la spirale - L, nombre de tours - n. Ces dimensions sont corrélées (voir les formules en-dessous du calculateur) et vous pouvez en calculer deux à partir de trois autres.
Nous pouvons voir les spirales dans la vie de tous les jours dans tous les objets en forme de cylindre : rouleau de papier, scotch, films et autres. Vous pouvez facilement trouver certaines dimensions de ces objets telles que les diamètres et l'épaisseur ou le nombre de tours et, en utilisant le calculateur ci-dessous, calculer celles qui manquent. Par exemple, vous pouvez calculer la longueur du rouleur à partir des diamètres internes et externes et de l'épaisseur du rouleau ou du nombre de tours. Vous pouvez également résoudre un problème inverse (lorsque vous connaissez la longueur du rouleau) - calculer l'épaisseur et le nombre de tours en utilisant la longueur du rouleau et les deux diamètres. La théorie et les formules sont, comme d'habitude, en-dessous du calculateur.
Veuillez faire attention au contrôle des unités lorsque vous saisissez les dimensions connues ! 20 mètres ne sont pas pareils que 20 millimètres...
Spirale d'Archimède
La spirale d'Archimède (également connue comme la spirale arithmétique) est une spirale correspondant aux localisations au cours du temps d'un point M s'éloignant d'un point central O avec une vitesse constante le long de la ligne OA qui tourne autour du point central O avec une vitesse angulaire constante.

Si nous désignons la distance de O à M comme ρ, et l'angle de rotation comme φ, alors nous pouvons décrire une spirale avec l'équation polaire :
,
où k est le paramètre taille, qui est égal au changement de distance lorsque l'angle pivote de 1 radian. Après un tours (un angle augmente de 2π), la distance augmente de 2πk.
Cette augmentation est la distance entre deux bras d'une spirale, la distance de séparation ou l'épaisseur de la spirale. Nous pouvons réécrire notre équation initiale en utilisant a :
Comme l'épaisseur est constante, plus le point M s'éloigne du centre, plus la spirale ressemble au cercle.
Pour dériver la formule de la longueur de la spirale, nous examinerons le changement infinitésimal de la longueur.
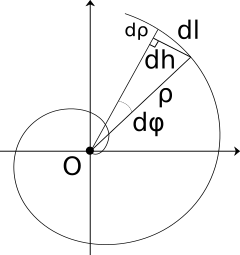
Un segment infinitésimal de la spirale dl peut être vu comme l'hypothénuse du triangle dl, dρ, et dh. Ainsi :
Un segment infinitésimal de la spirale dh peut être remplacé par un segment infinitésimal d'une cercle de rayon ρ ; ainsi sa longueur est ρdφ.
En utilisant l'équation polaire d'une spirale, nous pouvons remplacer ρ par kφ, et dρ par kdφ
Nous avons désormais le dépendance de la longueur dl par rapport à l'angle dφ. Pour trouver la longueur, nous devons intégrer l'angle initial à l'angle final.
Pour abréger, l'intégration finale est :
Si une spirale commence à un angle de zéro (à partir du centre), la formule est simplifiée :
Mais bien sûr, dans la vraie vie, un rouleau de matériel ne commence pas à partir du centre. Il a généralement un manchon, ainsi un diamètre interne et un angle initial. Comment tous ces paramètres sont-ils corrélés ?
Voici comment le nombre de tours n est corrélés aux angles :
Et voici comment les diamètres sont corrélés aux angles (ceci découle directement de l'équation polaire de la spirale)
Voici toutes les formules dont nous avons besoin pour trouver les dimensions inconnues selon les dimensions connues. Notez cependant que l'équation de la longueur est transcendentale, et la tâche inverse (trouver les dimensions inconnues alors que la longueur fait parti des dimensions connues) nécessite des méthodes numériques. Ce calculateur utilise la Méthode de la sécante.
commentaires