Calculateur de la longueur de l'arc
Ce calculateur en ligne universel peut trouver la longueur de l'arc d'un segment circulaire selon le rayon et l'angle, selon la corde et la hauteur et selon le rayon et la hauteur.
Cette page existe grâce aux efforts des personnes suivantes :
 | Timur
|
Gaulthier Marrel
|
Ce contenu est sous License Creative Commons Attribution/Partage à l'Identique 3.0(Unported). Cela signifie que vous pouvez redistribuer ou modifier librement ce contenu avec les mêmes modalités de licence et que vous devez créditer l'auteur original en plaçant un lien hypertexte de votre site vers l'œuvre https://fr.planetcalc.com/8336/. Vous ne pouvez pas modifier (le cas échéant) les références dans le contenu de l'œuvre originale.
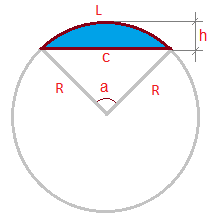
Ce calculateur en ligne calcule la longueur de l'arc d'un segment circulaire, suivant soit le rayon et l'angle du segment, soit la longueur de la corde et la hauteur du segment, soit le rayon et la hauteur su segment. Selon moi, la chose la plus utile est la capacité de trouver la longueur de l'arc selon la longueur de la corde et la hauteur - elles peuvent souvent être mesurées directement (voir l'image - la partie en bleu est le segment circulaire dont la longueur de l'arc doit être trouvée).
Dans le calculateur ci-dessous, choisissez les données que vous avez pour trouver la longueur de l'arc, saisissez-les et obtenez le résultat. Toutes les formules utilisées pour les calculs sont listées en-dessous du calculateur.
Calculateur de la longueur de l'arc
Trouver la longueur de l'arc selon le rayon et l'angle du segment circulaire
La formule est simple :
Trouver la longueur de l'arc selon la longueur de la corde et la hauteur du segment circulaire
Ici, vous devez calculer le rayon et l'angle et ensuite utiliser la formule ci-dessus.
Le rayon :
L'angle :
Trouver la longueur de l'arc selon le rayon et la hauteur du segment circulaire
Si vous devez calculer l'angle, alors utilisez à nouveau la formule .
L'angle :
Pour le calculateur universel concernant le segment circulaire en général, consultez le calculateur Segment circulaire. Il trouve la longueur de la corde, la hauteur du segment, le périmètre du segment, la surface du segment et la longueur de l'arc en fonction de vos données.
commentaires