Calculatrice en ligne: Volume d'un réservoir cylindrique incliné

Pour réaliser le calcul, vous devez fournir la taille du réservoir, l'angle et le niveau de liquide.

Mesure du niveau de liquide

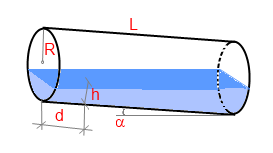
Vous devez mesurer le niveau de liquide à la ligne médiane perpendiculaire au réservoir jusqu'au fond du réservoir (voir image). Vous pouvez mesurer le niveau de liquide à n'importe quelle distance de l'une des bases (Si vous faites ceci, vous devez saisir la distance dans un paramètre spécial).
Sinon, vous pouvez incliner le réservoir pour avoir un niveau de liquide nul à la base supérieure. Dans ce cas, vous devez uniquement mesurer l'angle d'inclinaison.

Vous pouvez trouver les détails du calcul et les formules en-dessous du calculateur.

Volume de liquide dans un réservoir cylindrique incliné

Longueur du cylindre

Rayon du cylindre

Angle d'inclinaison (degrés)

Niveau du liquide

Niveau mesuré près de

base supérieure

base inférieure

Distance depuis la base

Distance entre la mesure du niveau de liquide et la base la plus proche. (0 si le niveau est mesuré juste à côté de la base).

Précision de calcul

Chiffres après la virgule décimale : 2

Niveau du liquide près de la base supérieure

Niveau du liquide près de la base inférieure

Longueur de la partie partiellement remplie du réservoir

Longueur de la partie complètement remplie du réservoir

Volume de liquide

Je n'ai pas pu trouver de solution toute prête pour calculer le volume de liquide d'un cylindre incliné, donc j'ai dérivé la formule de cette manière :

Formule du volume dun réservoir incliné partiellement rempli.

$V = \frac{R^2}{2}\int_{\small0}^L {\theta(x)-\sin{\theta(x)}dx$
où $\theta(x)$ - comment l'angle du segment dépend de la longueur du cylindre x,
Il peut être dérivé comme :
$\theta(x)=2\arccos{\frac{R-h}{R}}=2\arccos{\frac{R-(x\tan{\alpha}+h_{0})}{R}}$
où
a - angle d'inclinaison,
h0 - niveau de liquide à la base supérieure

Si nous substituons cette expression dans la formule, nous obtenons :
$V = R^2\int_{\small0}^L {\arccos{u}-u\sqrt{1-u^2}dx=-\frac{R^3}{\tan{\alpha}}\int_{\small{u_0}}^{u_L} {\arccos{u}-u\sqrt{1-u^2}du$
où $u=\frac{R-(x\tan{\alpha}+h_{0})}{R}$

Si nous prenons l'intégrale, nous obtenons la solution :
$V = -\frac{R^3}{\tan{\alpha}}\left( u\arccos{u}-\frac{1}{3}\sqrt{1-u^2}(u^2+2)\right)\large|_{\small{u_0}}^{u_L}$
$= \frac{R^3}{\tan{\alpha}}\left( K\arccos{K}-\frac{1}{3}\sqrt{1-K^2}(K^2+2)-{C}\arccos{C}+\frac{1}{3}\sqrt{1-C^2}\left(C^2+2\right) \right)$

où
$K=1-\frac{h_{0}}{R}$ ,
$C=K-\frac{{L}tan{\alpha}}{R}$

Déterminer la longueur du réservoir remplie de liquide

Les formules ci-dessus sont utilisées pour le calcul du volume d'un réservoir incliné avec les hypothèses suivantes :

Les deux bases sont partiellement remplies de liquide.
Le niveau de liquide h₀ est mesuré directement à la base supérieure.
Aucune partie du réservoir n'est sèche ou remplie complètement.

Mais le calculateur accepte le niveau de liquide mesurée à une distance proche de la base supérieure ou inférieure. Certaines parties du réservoir peuvent être sèches ou complètement remplies.

Pour calculer le niveau de liquide directement à la base supérieure h_u utiliser les formules :
$h_u=h_{ll}-(L_c-l_l){\tan{\alpha}}$
où h_ll - niveau de liquide mesuré à la distance l_l de la base inférieure, L_c - longueur du réservoir
$h_u=h_{lu}-l_u{\tan{\alpha}}$
où h_lu - niveau de liquide mesuré à la distance l_u de la base supérieure.
Si h_u est égal ou supérieur à zéro, nous supposons que h₀=h_u, et que L_f = L_c.

Partie vide du réservoir

Sinon, h_u peut être négative. Ceci signifie que certaines parties du réservoir sont vide. Dans ce cas, estimer
h₀=0 et calculer la partie restante (remplie) L_f en utilisant la formule :
$L_f=L_c+\frac{h_u}{\tan{\alpha}}$
où L_c est la longueur du cylindre.

Partie complètement remplie.

Le niveau de liquide directement à la base inférieure h₁ peut être déterminé comme :
$h_1=h_0+L_f{\tan{\alpha}}$
Si la valeur h₁ calculée est supérieure au diamètre du réservoir, certaines parties de notre cylindre sont complètement remplies de liquide. Ainsi, nous avons besoin de calculer la longueur des parties complètement remplies comme :
$L_t=\frac{h_1-2{R}}{\tan{\alpha}}$
Le calcul de la partie complètement remplie est trivial, voir Cylindre

Après ces calculs, vous pouvez substituer la longueur partiellement remplie du réservoir $L=L_f-L_t$ et le niveau de liquide h₀ dans les formules de la première section pour calculer le volume partiellement rempli d'un réservoir incliné.

PLANETCALC Calculatrices en ligne

Volume d'un réservoir cylindrique incliné

Cette page existe grâce aux efforts des personnes suivantes :

Anton

Gaulthier Marrel

Mesure du niveau de liquide

Volume de liquide dans un réservoir cylindrique incliné

Formule du volume dun réservoir incliné partiellement rempli.

Déterminer la longueur du réservoir remplie de liquide

Partie vide du réservoir

Partie complètement remplie.

Calculatrices similaires

commentaires

PLANETCALC Calculatrices en ligne

Mesure du niveau de liquide

Volume de liquide dans un réservoir cylindrique incliné

Formule du volume dun réservoir incliné partiellement rempli.

Déterminer la longueur du réservoir remplie de liquide

Partie vide du réservoir

Partie complètement remplie.

Calculatrices similaires

commentaires

Partager la page