Longueur de l'arc parallèle
Cette calculatrice en ligne convertit la longueur d'arc d'un parallèle à une latitude donnée, de degrés en mètres.
Cette page existe grâce aux efforts des personnes suivantes :
 | Timur
|
Milena
|
Nous avons une calculatrice qui calcule longueur de l'arc méridien en fonction de la latitude, plus précisément la longueur de l'arc méridien d'une minute, plus connu sous le nom de mille marin. Pour être complet, j'ai décidé d'écrire une calculatrice qui calcule la taille de l'arc parallèle en fonction de la latitude. D'après des considérations assez évidentes, plus la latitude est grande, c'est-à-dire plus nous sommes proches de tel ou tel pôle, plus la taille de l'arc, disons de 1 degré, en mètres, est petite. La calculatrice ci-dessous calcule la taille de cet arc à une latitude donnée en fonction de la taille angulaire de l'arc. À titre de référence, à l'équateur, la taille de l'arc d'un parallèle d'un degré serait maximale (la latitude est nulle) et serait de 111 km 319 mètres (approximatif). La méthode de calcul est décrite dans la calculatrice.
Longueur de l'arc parallèle
Longueur de l'arc du parallèle
Le calcul est assez simple et s'effectue à partir de considérations géométriques générales. Bien entendu, la Terre est approximativement une sphère (bien qu'il s'agisse d'un géoïde).
Pour trouver la longueur de l'arc d'un cercle par l'angle d'arc α, il suffit de multiplier le rayon du cercle r par l'angle d'arc en radians
.
Pour un arc de 360 degrés, soit 2π radians, la formule se transforme en la formule bien connue de la longueur d'un cercle
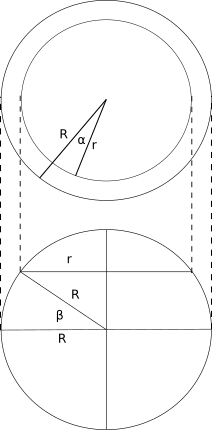
Comme le montre la figure, à une certaine latitude, nous nous intéressons au rayon du cercle r, obtenu en coupant une partie de la sphère par un plan parallèle au plan de l'équateur. A l'équateur même, le rayon coïncide avec le rayon de la terre R. Exprimons le rayon qui nous intéresse par le rayon de la Terre R et la latitude β donnée :
.
En conséquence, la formule finale
Et comme rayon de la Terre, nous prenons la valeur définie dans la norme WGS-84, à savoir 6378137m. C'est tout.
commentaires