Calculatrice en ligne: Condensateur dans un circuit en courant continu

Ces calculateurs en ligne calculent divers paramètres pour la charge et la décharge d'un condensateur avec une résistance. Les formules utilisées pour les calculs sont en-dessous des calculateurs.

Charge d'un condensateur avec une résistance

Tension d’alimentation, Volts

Résistance, Ohms

Valeur du condensateur, microFarads

Temps de charge, millisecondes

Précision de calcul

Chiffres après la virgule décimale : 2

Constante de temps, millisecondes

5 Constantes de temps (99,2 % chargé), millisecondes

Courant initial, Ampères

Dissipation de puissance maximale, watts

Tension du condensateur, Volts

Charge du condensateur, microCoulombs

Energie du condensateur, milliJoules

Alimentation électrique, milliJoules

Décharge d'un condensateur avec une résistance

Tension initiale du condensateur, Volts

Résistance, Ohms

Valeur du condensateur, microFarads

Temps de décharge, millisecondes

Précision de calcul

Chiffres après la virgule décimale : 2

Energie initiale du condensateur, milliJoules

Charge initiale du condensateur, microCoulombs

Constante de temps, millisecondes

Courant initial, Amprères

Dissipation de puissance maximale, watts

Charge finale du condensateur, microCoulombs

Energie finale du condensateur, milliJoules

Tension finale du condensateur, Volts

Voici ci-dessous l'image d'un circuit électrique pour la charge d'un condensation avec une unité d'alimentation électrique.

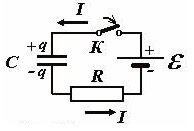
Lorsque l'interrupteur K est fermé, le courant direct commence à charger le condensateur.
Selon la loi d'OHm, la somme des tensions du condensateur et de la résistance est égale à la tension de l'alimentation électrique.
$\epsilon=IR+\frac{q}{C}$
La charge du condensateur et le courant dépendent de la durée. Au moment initial, il n'y a pas de charge dans le condensateur, ainsi le courant est maximal ainsi que la dissipation de puissance de la résistance.
$I=\frac{\epsilon}{R}, P=I^2R$
Durant la charge, la tension du condensateur varie selon l'équation suivante
$V(t)=\epsilon(1-e^{-\frac{t}{RC}})$
où tau
$\tau=RC$
est appelé Constante de temps. Puisque la charge est un processus infini, un condensateur est généralement considéré comme complètement chargé après 5 Constantes de temps. Après 5 constantes de temps, le condensateur sera chargé à 99,2 % de la tension d'alimentation.
Charge du condensateur
$Q=CV$
Energie du condensateur
$W=\frac{Q^2}{2C}$
Alimentation électrique
$A=Q\epsilon$