Segment circulaire
Peut calculer la surface, la longueur de l'arc, la longueur de la corde et le périmètre d'un segment circulaire suivant le rayon et l'angle.
Ce contenu est sous License Creative Commons Attribution/Partage à l'Identique 3.0(Unported). Cela signifie que vous pouvez redistribuer ou modifier librement ce contenu avec les mêmes modalités de licence et que vous devez créditer l'auteur original en plaçant un lien hypertexte de votre site vers l'œuvre https://fr.planetcalc.com/1421/. Vous ne pouvez pas modifier (le cas échéant) les références dans le contenu de l'œuvre originale.
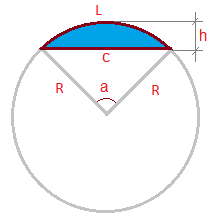
Le segment circulaire - est la surface d'un cercle qui est "séparée" du reste du cercle par une sécante (corde).
Sur l'image :
L - longueur de l'arc
h- hauteur
c- corde
R- rayon
a- angle
Si vous connaissez le rayon et l'angle, vous pouvez utiliser les formules suivantes pour calculer les autres paramètres du segment :
Formules du segment circulaire
Surface :
[1]
Longueur de l'arc :
Longueur de la corde :
Hauteur du segment :
Segment circulaire
Néanmoins, si vous ne connaissez pas le rayon et l'angle, vous pouvez toujours calculer les paramètres su segment suivant la longueur de la corde et la hauteur du segment :
Segment défini par la corde et la hauteur
Formule pour le rayon du segment suivant la corde et la hauteur :
Ensuite, vous pouvez calculer l'angle du segment en utilisant la formule suivante :
Vous pouvez également utiliser le calculateur suivant pour obtenir la surface su segment suivant son rayon et sa hauteur :
Surface d'un segment circulaire avec un rayon et une hauteur
Ce calculateur évalue l'angle grâce à la formule suivante :
ensuite, il utilise la formule [1] pour calculer la surface du segment.
commentaires